在三条指令内实现闰年判断

发表于 2025年5月29日 20:29 更新于 2025年5月29日 22:55 分类于源码分析阅读次数：

本文是A leap year check in three instructions的翻译，前两天在HackerNews上看到这篇文章，闰年的判断方法，从一开始学编程就是一个经典的练习题，但是深挖下去，作者只用了三条指令就能实现闰年的判断，感觉还挺有意思的，所以就翻译分享一下。

省流不看版（基于DeepSeek总结）：
文章介绍了一种使用大约3个CPU指令实现快速闰年检查的方法。这种方法不同于标准算法（涉及模运算和分支），而是利用位操作和魔法数字，将闰年规则（能被4整除，但不能被100整除，除非能被400整除）巧妙地映射到对年份乘以一个常数后的结果进行位范围检查。这种位操作方法对于随机年份输入表现出显著的速度提升，并且针对特定范围已证明是最优解。这项优化技术涉及复杂的位运算细节。

以下是原文的翻译：

通过以下代码，我们可以在大约 3 个 CPU 指令内检查 0 ≤ y ≤ 102499 的年份是否是闰年：

bool is_leap_year_fast(uint32_t y) {
    return ((y * 1073750999) & 3221352463) <= 126976;
}

这是如何工作的呢？答案出奇地复杂。本文解释了其中的原理，主要是为了享受位操作的乐趣；最后，我将简要讨论其实际用途。我们一般使用的基础版闰年检查代码是这样的：

bool is_leap_year(uint32_t y) {
    if ((y % 4) != 0) return false;
    if ((y % 100) != 0) return true;
    if ((y % 400) == 0) return true;
    return false;
}

我们使用的是前推格里高利历，它将格里高利历从1582年引入的时间向前延伸，并包含0年。因此，我们无需对1582年之前的年份做特殊处理。为简化起见，我们忽略负数年份，使用无符号年份。

标准方法的优化

我们先做一些简单的优化，以便获得一个良好的基准线。我不确定应该把功劳归给谁，这些技巧可能已经被独立实现很多次了。
我们可以将(y % 100) != 0替换为(y % 25) != 0：我们已经知道y是2²的倍数，所以如果它也是5²的倍数，它就是2² * 5² = 100的倍数。类似地，我们可以将(y % 400) == 0替换为(y % 16) == 0：我们已经知道y是5²的倍数，所以如果它也是2⁴的倍数，它就是5² * 2⁴ = 400的倍数：

bool is_leap_year1(uint32_t y) {
    if ((y % 4) != 0) return false;
    if ((y % 25) != 0) return true;
    if ((y % 16) == 0) return true;
    return false;
}

这很有用，因为我们现在可以用位掩码替换对 4 和 16 的取余运算。还有一个编译器实现者熟知的技巧，可以将对 25 的取余运算降低成本。用 gcc 编译(x % 25) != 0并翻译回 C，我们得到x * 3264175145 > 171798691。乘法在典型的延迟约为 3 个周期，而取余运算至少需要 20 个周期，这是一个巨大的改进。我只会简要说明其工作原理的直觉；更多细节可以在以下资源中找到：

Faster remainder by direct computation: Applications to compilers and software libraries by Daniel Lemire, Owen Kaser, and Nathan Kurz for lowering modulo by a constant in general;
Euclidean affine functions and their application to calendar algorithms by Cassio Neri and Lorenz Schneider more specifically for calendar calculations; and
Identifying leap years by David Turner for the leap year check (including formal proofs!).

关于3264175145和171798691这两个”magic numbers”是从哪里来的呢？我们有

2³² * 19/25 = 3264175144.96 (这个是精确值)
因此，通过乘以3264175145，我们可以近似得到乘以 (19/25) 的小数部分，如果是乘以3264175144.96这个精确值的话，对于25的倍数，我们将得到一个整数。但实际乘的数是比精确值大了0.04，因此会有最大0.04 * (2³² - 1) = 171798691.8的误差，这也是171798691的来源。

这个技巧对于x % 100效果不太好，需要多一条修正指令，所以从y % 100减少到y % 25还是有必要的。

到这里，我们的代码变成了这样：

bool is_leap_year2(uint32_t y) {
    if ((y & 3) != 0) return false;
    if (y * 3264175145u > 171798691u) return true;
    if ((y & 15) == 0) return true;
    return false;
}

需要注意的是，像 gcc 或 clang 这样的现代编译器会从 is_leap_year1 生成类似 is_leap_year2 的代码，因此在 C 源代码中这样做意义不大，但在其他编程语言中可能还是有用的。
这段代码通常会被编译成带分支跳转的汇编代码。然而实际上这个函数的输入通常是可预测的，所以这不一定是坏事。如果我们想在牺牲最好场景下的性能来避免大部分场景下分支预测失败的开销的话，我们可以稍微调整一下顺序，得到无分支跳转的代码：

bool is_leap_year3(uint32_t y) {
    return !(y & ((y % 25) ? 3 : 15));
}

当然如果您想了解更多日历计算相关的加速方法，可以查阅 Jacob Pratt 的Optimizing with Novel Calendrical Algorithms。

寻找基于位操作的方法

我们能否通过放弃对所有输入的正确性来改进闰年计算？毕竟，我们通常不关心年份3584536493是否是闰年；实际上，Python、C# 和 Go 只支持 0 年（或 1 年）到 9999 年（此时相对于季节的漂移已经超过 4 天）。我的想法是，如果存在更短的形式，它基本上会像使用魔术常数进行某种奇怪的哈希操作，所以我尝试了一些方法，并通过暴力搜索猜测常数。(y * f) <= t的形式似乎有用，但不够强大。我的一个备选方案是添加一个掩码：((y * f) & m) <= t。现在我们需要猜测 96个bit位，这无法单独通过暴力搜索完成。让我们使用z3，一个支持位向量约束的求解器，它非常适合这项工作。

import z3

BITS = 32
f, m, t, y = z3.BitVecs('f m t y', BITS)

def target(y):
    return z3.And((y & 3) == 0, z3.Or(z3.URem(y, 25) != 0, (y & 15) == 0))

def candidate(x):
    return z3.ULE((x * f) & m, t)

solver = z3.Solver()
solver.add(z3.ForAll(y, z3.Implies(z3.ULE(y, 400),
                                   candidate(y) == target(y))))

if solver.check() == z3.sat:
    print(f'found solution: {solver.model()}')
else:
    print('no solution found')

在几秒钟内，这找到了一些常数，它们在一定年份范围内给出了正确的结果。扩展范围后，大约花费了半小时的计算时间，我最终找到了在0年到102499年范围内给出正确结果的常数，并证明了这是32位的最优解：

bool is_leap_year_fast(uint32_t y) {
    const uint32_t f = 1073750999u;
    const uint32_t m = 3221352463u;
    const uint32_t t = 126976u;
    return ((y * f) & m) <= t;
}

解释

它是如何工作的呢？我们能将所有这些计算压缩到三条指令中，这似乎令人惊讶，感觉就像是魔法一样，不过，上面的内容已经给我们足够多的工具来理解它了。

下面是这三个常量的二进制表示，并且用ABCD标识出来了相关的bit范围：

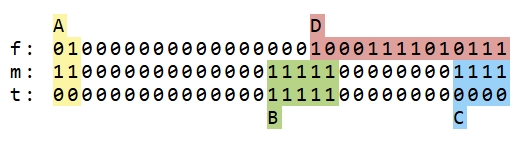
让我们首先考虑乘积 p := y * f，与 m 进行位与操作后再和t进行比较的作用。在区块 A 中，t 的位为 0，因此只要 p 中 A 中的任何位被设置，结果就为 false。否则，区块 B 就变得相关。在这里，t 中的所有位都为 1，所以只要 p 中 B 中的任何位未设置，结果就为 true。否则，对于区块 C，我们要求 p 中所有位都未设置。通过这种方式，多个位范围的比较都被统一到一个单一的 <= 操作中。因此，我们可以将 is_leap_year_fast 重写如下：

bool is_leap_year_fast2(uint32_t y) {
    uint32_t p = y * 1073750999u;
    const uint32_t A = 0b11000000000000000000000000000000;
    const uint32_t B = 0b00000000000000011111000000000000;
    const uint32_t C = 0b00000000000000000000000000001111;
    if ((p & A) != 0) return false;
    if ((p & B) != B) return true;
    if ((p & C) == 0) return true;
    return false;
}

这看起来非常像is_leap_year2！实际上，这三个条件的目的是完全相同的。我们可以证明：

当(p & A) != 0时，(y % 4) != 0 也成立；
当(p & B) != B时，(y % 100) != 0也成立；
当(p & C) == 0时，(y % 16) == 0（而且 (y % 400) == 0，因为我们已经知道 y 是25的倍数）。

针对（1）和（3）这两种简单场景：

(1)：f 中 A 的1位将 y 的低两位重现在 p 的 A 位置。这不会被与 D 中的位相乘的结果所破坏：我们能得到的最大值是 102499 * (f & D) = 940428325，它只有30位。因此，检查 p 中 A 是否为零等同于检查 y 是否模4为0。
(3)：检查 p 的最低4位是否都未设置，就是检查 p 是否模16为0。然而，我们实际想检查的是 y。这不是问题：只需查看 f 的最低4位即可，而 f 在那里是1111₂ = 7。乘以7不会引入额外的因数2，因此依然是可以被16整除的。

针对（2）这种有趣的场景：

接下来，让我们尝试找出哪些数满足 p & B ≠ B。为此，f & A 中的1位不起作用，所以考虑 f & D 中的位。它们是 10001111010111₂ = 9175。让我们看看哪些数通过了测试：

>>> B = 0b00000000000000011111000000000000
>>> s = [y for y in range(5000) if ((y * 9175) & B) == B]
>>> for i in range(0, len(s), 16): print(*(f'{n:4d}' for n in s[i:i+16]))
  14   57   71  100  114  157  171  200  214  257  271  300  314  357  371  400
 414  457  471  500  514  557  571  600  614  657  671  700  714  757  771  800
 814  857  871  900  914  957  971 1000 1014 1057 1071 1100 1114 1157 1171 1200
1214 1257 1271 1300 1314 1357 1371 1400 1414 1457 1471 1500 1514 1557 1571 1600
1614 1657 1671 1700 1714 1757 1771 1800 1814 1857 1871 1900 1914 1957 1971 2000
2014 2057 2071 2100 2114 2157 2171 2200 2214 2257 2271 2300 2314 2357 2371 2400
2414 2457 2471 2500 2514 2557 2571 2600 2614 2657 2671 2700 2714 2757 2771 2800
2814 2857 2871 2900 2914 2957 2971 3000 3014 3057 3071 3100 3114 3157 3171 3200
3214 3257 3271 3300 3314 3357 3371 3400 3414 3457 3471 3500 3514 3557 3571 3600
3614 3657 3671 3700 3714 3757 3771 3800 3814 3857 3871 3900 3914 3957 3971 4000
4014 4057 4071 4100 4114 4157 4200 4214 4257 4300 4314 4357 4400 4414 4457 4500
4514 4557 4600 4614 4657 4700 4714 4757 4800 4814 4857 4900 4914 4957

正如所愿，100的倍数在这里出现了，但也出现了一堆其他的数字。但只要它们都不是4的倍数都没关系，因为这些数字会在前一步里先被被过滤掉。另外，0不见了，但这也不是问题，因为0也是400的倍数。

让我们试着理解这个规律。乍一看，它看起来非常简单：我们有 *14, *57, *71 和 *00。然而，从4171开始，*71 就消失了（你注意到了吗？）。后面也有新的规律出现。让我们再借助Python来分析一下：

def test(y):
    B = 126976
    return ((y * 9175) & B) == B

active = set()
for y in range(120000):
    r = y % 100
    if test(y):
        if r not in active:
            print(f'{y:6}: started *{r:02}')
            active.add(r)
    else:
        if r in active:
            print(f'{y:6}: stopped *{r:02}')
            active.remove(r)

可以得到：

    14: started *14
    57: started *57
    71: started *71
   100: started *00
  4171: stopped *71
 32843: started *43
 36914: stopped *14
 65586: started *86
 69657: stopped *57
 98329: started *29
102500: stopped *00

所以，从102500开始，我们不再捕获100的倍数，这解释了为什么102499是is_leap_year_fast能获得正确结果的最后一个数字。我们还看到，在此之下，除了100的倍数外，没有其他数字是4的倍数（方便的是，我们只需知道最后两位十进制数字就可以检查这一点）。如果信任这种暴力枚举的结果，这就完成了条件(2)的证明；但我们继续更深入地理解为什么我们恰好得到了这些数字。

让我们深入研究一下为什么我们首先得到了100的倍数。因子9175在17位定点表示中接近于1/100的倍数：

2¹⁷ * 7/100 = 9175.04 (这个是精确值)。

将100的倍数乘以9175.04，会得到一个整数（7的倍数），位于第17位及以上，以及低于第17位的17个零位，例如：
9175.04 * 500 = 10001100000000000000000₂, 其中100011₂ = 35 = 5 * 7。

将100的倍数乘以9175会得到略小的结果：
9175 * 500 = 10001100000000000000000₂ − 500 * 0.04 = 10001011111111111101100₂

一般来说，从一个以很多零结尾的数字中减去一点点，除了末尾的0之外，会得到一个以很多一结尾的数字。在这里，我们检查 B 中的5位。对于 y 是100的倍数，这些位保证都是1，随着误差慢慢累计累积达到 B 的低位，这只有在 y = 2¹⁷ / 0.04 = 102400之后才会发生，所以这是符合预期的。

那么像14、57、71这样的其他数字是从哪里来的呢？让我们换个角度来看：
我们有 9175 = 2¹⁷ * 0.06999969482421875 (精确值)，而 B = 2¹⁷ * 0.96875，所以：
p & B = B ⇔ {y * 0.06999969482421875} ≥ 0.96875 其中 {x} 是 x 的小数部分 ⇔ 6.999969482421875y mod 100 ≥ 96.875

这也同样解释了为什么100的倍数是可以的：对于100的倍数，7y mod 100 是 0，所以 6.999969482421875y mod 100 会稍微小于 100，并且只有在 y = (100 − 96.875) / (7 − 6.999969482421875) = 102400 之后才会降到 96.875 以下。

为了理解在我们序列中出现的其他数字，让我们首先考虑如果我们在不等式中是整数 7，解会是什么：
7y mod 100 ≥ 96.875 ⇔ 7y mod 100 ∈ {97, 98, 99}。

为了找到这个解，我们首先需要 7 mod 100 的模逆元，也就是说，一个数字 x 使得 7x mod 100 = 1。我们可以使用扩展欧几里德算法计算它，或者直接使用在线计算器，它会告诉我们结果是 43。那么解就是 43 * 97 (mod 100)，43 * 98 (mod 100)，以及 43 * 99 (mod 100)，结果分别为 71、14 和 57 (mod 100)。这解释了为什么我们最初会看到 *14、*57 和 *71 形式的数字。这也解释了为什么我们在 4071 之后不再看到 *71 等数字：虽然 7 * 4171 = 29197，但我们有 6.999969482421875 * 4171 = 29196.872711181640625，它（模 100）小于 96.875。类似地，32843 出现是因为累积误差 (7 − 6.999969482421875) * 32843 = 1.002288818359375 超过了1。再花一些精力，我们就可以手动重现上面的 Python 程序的输出，并检查这些数字中没有任何一个是4的倍数。

扩展到其他比特位

现在我们理解了这个技巧的工作原理，我们可以尝试为其他比特位寻找参数，可变部分是区块B，以及 f & D 中100的小数部分：

uint64_t score(uint64_t f, uint64_t m, uint64_t t) {
      for (uint64_t y = 0; ; y++)
          if ((((y * f) & m) <= t) != is_leap_year(y))
              return y;
  }
  
  int main() {
      uint64_t best_score = 0;
      for (int k = 0; k < BITS; k++) {
          for (int k2 = 0; k2 < k; k2++) {
              uint64_t t = (1ULL << k) - (1ULL << k2);
              uint64_t m = (0b11ULL << (BITS - 2)) | t | 0b1111;
              for (int n = 0; n < 100; n++) {
                  uint64_t f = (0b01ULL << (BITS - 2)) | (((1ULL << k) * n) / 100);
                  uint64_t new_score = score(f, m, t);
                  if (new_score > best_score) {
                      printf("%llu %llu %llu: %llu (%d %d %d)\n",
                             f, m, t, new_score, k, k - k2, n);
                      best_score = new_score;
                  }
              }
          }
      }
      return 0;
  }

对于BITS = 64的情况，花了大约7分钟，我们找到了 f = 4611686019114582671，m = 13835058121854156815，t = 66571993088，这个组合对于 y = 5965232499 及以下的年份是都正确的。这很棒，因为 5965232499 > 2¹⁷，所以任何32位整数年份都可以基于这个组合来计算。

对于64位来说，这是我们能达到的最好结果吗？也许还有其他常数效果更好？我无法立即找到证明方法，所以我采用了久经考验的方法——让别人为我做这件事，将其发布到Code Golf StackExchange上。果然，仅1小时后，用户ovs就发布了一个非常好的结果，两天后用户Exalted Toast发布了证明，表明5965232499确实是64位的最佳可能范围，同样的，他也使用了z3来进行求解。

性能测试

想要做一个有意义的基准测试不太容易，因为函数执行时间都非常短，而且对于普通带分支跳转的版本，执行时间和输入强相关。我们尝试了两个极端情况：只输入2025年，以及使用完全随机的年份。以下是在 i7-8700K (Coffee Lake, 4.7 GHz) 上使用g++ -O3 -fno-tree-vectorize编译的基准测试结果：

函数名称	2025 (ns)	random (ns)
is_leap_year	0.65	2.61
is_leap_year2	0.65	2.75
is_leap_year3	0.67	0.88
is_leap_year_fast	0.69	0.69

这个结果还是有些奇怪的地方的：

is_leap_year2在随机年份情况下比is_leap_year还要稍微慢一点。这有点奇怪，因为y % 100比is_leap_year2中的实现还要多一条指令。（根据Cassio Neri的评论，一个可能的解释是分支预测错误的概率差距导致，is_leap_year平均每100次预测错误一次，而is_leap_year2平均每25次预测就会错误一次。）
is_leap_year3在随机数据上比固定值慢一点。这也很奇怪，因为它没有任何分支跳转，理论上时间应该固定的。除了“基准测试很难”之外，我无法解释这一点。

从结果看，对于随机数据，新函数is_leap_year_fast比标准实现快 3.8 倍，对于完美可预测的输入，大约慢 6%。总的来说，这看起来相当不错。

总结

总结一下，这么做一个小优化是否真的值得？我们是否应该用这个新的函数替换现有的实现，比如将CPython datetime替换掉？嗯，这还是得根据实际情况决定。实践中查询的大多数年份会是当前年份，或者至少是相当可预知的年份，在这种情况下，我们并没有很大的优势。为了充分证明改变是合理的，理想情况下我们需要一个使用闰年检查作为子程序的实际数据基准测试，而不仅仅是微基准测试。我很乐意听到任何此类结果！